Introducción
Preguntas sobre el vídeo:
- ¿Qué dos tipos de aprendizaje no supervisado nombra en el vídeo?
- ¿En que consiste el aprendizaje semisupervisado?
Preguntas sobre el vídeo:
- ¿Por qué no nos vamos de viaje si no tenemos dinero?
- ¿Qué es un perceptrón? ¿Cuáles son sus partes?
- ¿Qué es un perceptrón multicapa?
- ¿Podemos ajustar manualmente los pesos de una neurona? ¿Y el umbral?
Preguntas sobre el vídeo:
- ¿Esconde la inteligencia artificial estructuras if/else “ocultas”? ¿Por qué?
- ¿Cuántas capas ocultas debe tener la red neuronal de ejemplo del vídeo?
- ¿Cada neurona de la capa de entrada se conecta con cada neurona de la primera capa oculta?
- ¿La red neuronal siempre funciona mejor con más datos de entrenamiento?
- ¿Se puede programar con estructuras if/else el ejemplo del vídeo?
Definición y esquema general de una red neuronal
¿Qué es una neurona?
Una neurona artificial es una función matemática concebida como un modelo de una neurona biológica. La neurona artificial recibe una o más entradas y las suma para producir una salida. Por lo general, cada entrada se pondera por separado con un peso y la suma se pasa a través de una función no lineal conocida como función de activación.
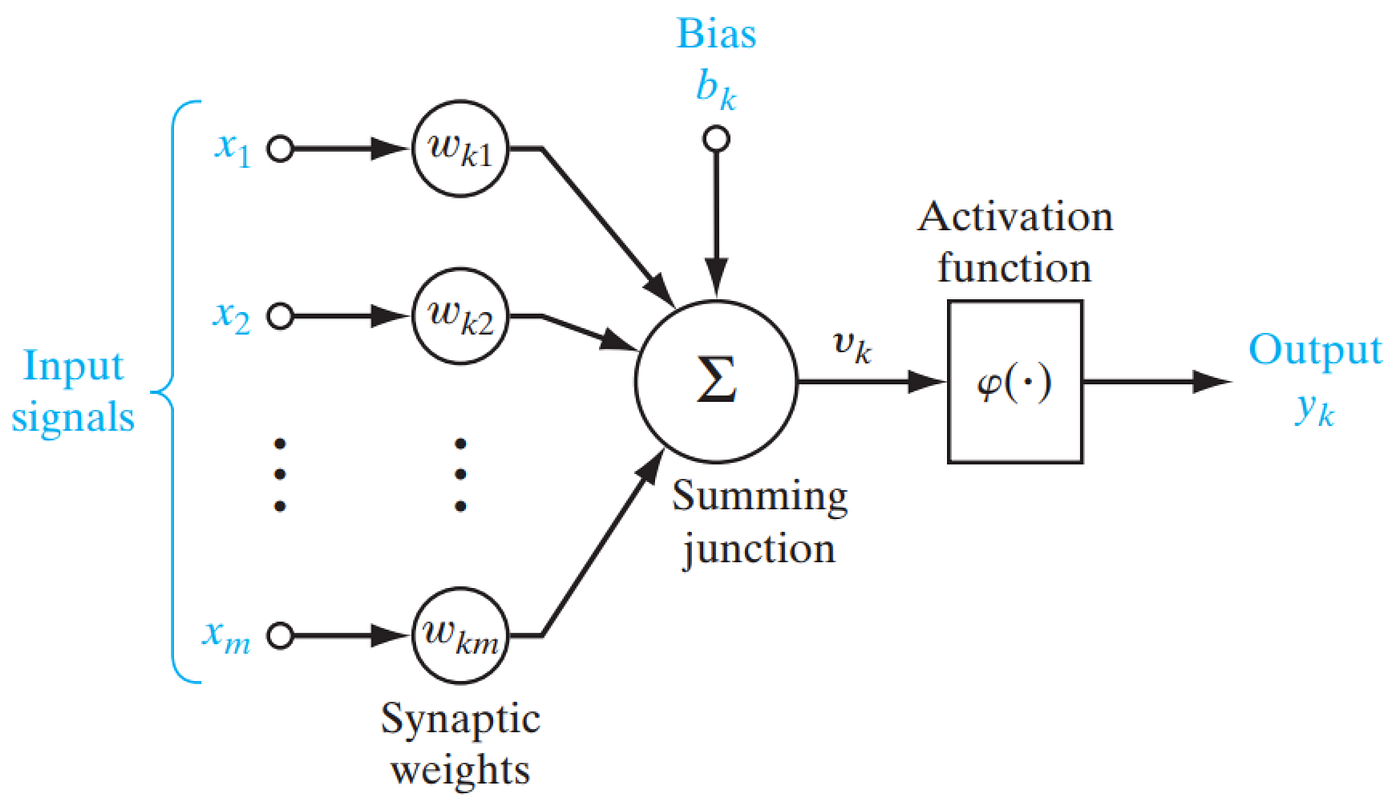Estructura básica de una neurona
¿Es lo mismo una neurona que un perceptrón?
¿Qué es una red neuronal?
Preguntas sobre el vídeo:
- ¿Es lo mismo una neurona artificial que una función matemática?
- ¿Cuál es la solución para resolver el problema de clasificación del XOR?
Preguntas sobre el vídeo:
- ¿Cuales son los 3 tipos de capas de una red neuronal?
- ¿Qué ocurre cuando sumamos varias líneas rectas entre si?
- ¿Qué funciones de activación nombra en DotCSV en el vídeo?
Las redes neuronales artificiales (llamadas simplemente redes neuronales) son sistemas informáticos inspirados en las redes neuronales biológicas que constituyen los cerebros de los animales.
Una red neuronal se basa en una colección de neuronas artificiales. Cada conexión, como las sinapsis en un cerebro biológico, puede transmitir una señal a otras neuronas. Una neurona artificial recibe señales, luego las procesa y puede enviar señales a las neuronas conectadas a ella. La “señal” en una conexión es un número real, y la salida de cada neurona se calcula mediante alguna función no lineal de la suma de sus entradas. Las redes neuronales artificiales (llamadas simplemente redes neuronales) son sistemas informáticos inspirados en las redes neuronales biológicas que constituyen los cerebros de los animales.
Una red neuronal se basa en una colección de neuronas artificiales. Cada conexión, como las sinapsis en un cerebro biológico, puede transmitir una señal a otras neuronas. Una neurona artificial recibe señales, luego las procesa y puede enviar señales a las neuronas conectadas a ella. La “señal” en una conexión es un número real, y la salida de cada neurona se calcula mediante alguna función no lineal de la suma de sus entradas.
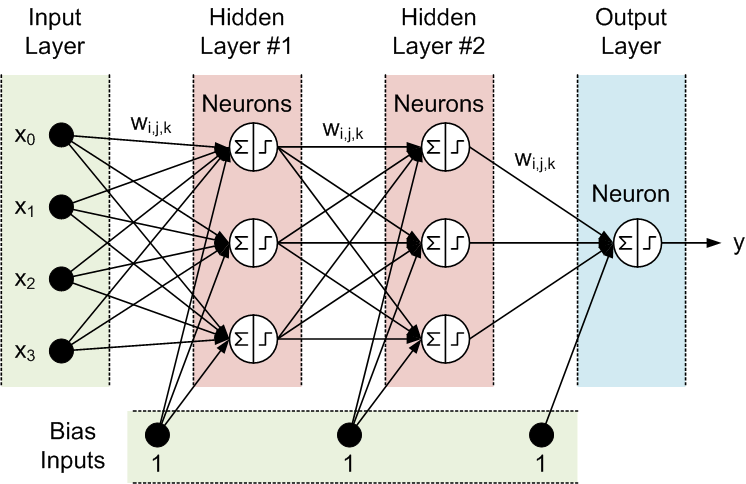Estructura de una red neuronal
¿Qué es el bias?
Funciones de activación
La función de activación determina, como su propio nombre indica, el nivel de activación que alcanza cada neurona una vez que ha recibido los impulsos transmitidos. Estas funciones ostentan un rol muy importante en la determinación del poder computacional de la red neuronal.
La función de activación se encarga de devolver una salida a partir de un valor de entrada, normalmente el conjunto de valores de salida en un rango determinado como (0,1) o (-1,1).
Se buscan funciones que las derivadas sean simples, para minimizar con ello el coste computacional.
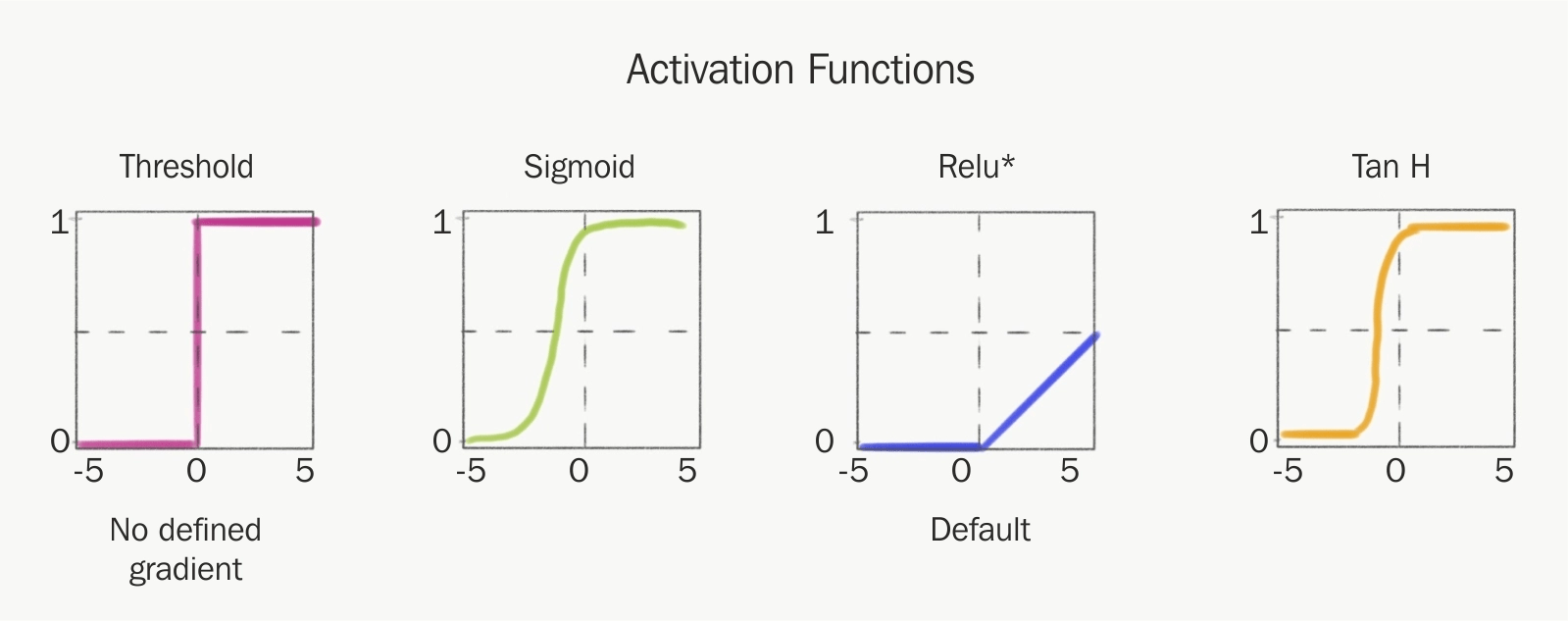Funciones de activación
Link muy explicativo sobre los diferentes tipos de funciones de activación: https://www.diegocalvo.es/funcion-de-activacion-redes-neuronales/.
Función de activación Softmax
En la teoría de la probabilidad, la salida de la función softmax se puede utilizar para representar una distribución categórica, es decir, una distribución de probabilidad sobre K diferentes resultados posibles. Por tanto, la función softmax se utiliza para clasificación multiclase. Podríamos considerar la función softmax como una generalización de la función sigmoid que permite clasificar más de dos clases. La función de activación softmax nos garantiza que todas las probabilidades estimadas son entre 0 y 1 y que suman 1.
A nivel matemático, softmax usa el valor exponencial de las evidencias calculadas y, luego, las normaliza de modo que sumen uno, formando una distribución de probabilidad.
\[\sigma: \mathbb{R}^K \to [0,1]^K\] \[\sigma(z_i) = \frac{e^{z_{i}}}{\sum_{j=1}^K e^{z_{j}}} \ \ \ for\ i=1,2,\dots,K\]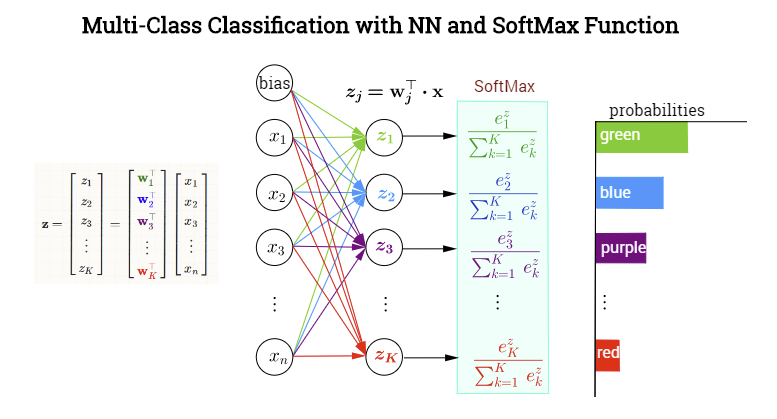
Ejemplo de la función de activación softmax
Sobreajuste
Algoritmos de redes neuronales
Deep Learning
El aprendizaje profundo es un tipo avanzado de aprendizaje automático dentro de las redes neuronales.
El aprendizaje profundo es un enfoque moderno basado en un modelo conceptual de cómo funciona el cerebro humano. El modelo (también llamado red neuronal) está compuesto por colecciones de neuronas (unidades computacionales muy simples) conectadas entre sí por pesos (representaciones matemáticas de cuánta información se permite que fluya de una neurona a la siguiente). Los pesos de estas conexiones codifican el conocimiento de una red. Estos pesos en los enlaces pueden incrementar o inhibir el estado de activación de las neuronas adyacentes. Del mismo modo, a la salida de la neurona, puede existir una función limitadora o umbral, que modifica el valor resultado o impone un límite que no se debe sobrepasar antes de propagarse a otra neurona. Esta función se conoce como función de activación.
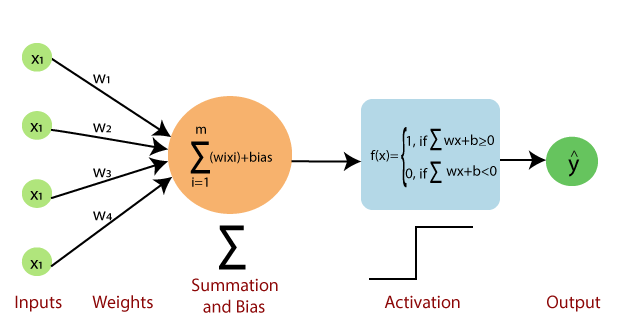Perceptrón
El proceso de entrenamiento implica encontrar valores para cada peso.
En la actualidad existen muchos tipos diferentes de redes neuronales para modelar diferentes tipos de problemas o procesar diferentes tipos de datos.
Una red neuronal profunda posee tres o más capas de redes neuronales internas (hidden) y tiene nodos neuronales anidados tal que por cada pregunta que responde conduce a un conjunto de preguntas relacionadas.
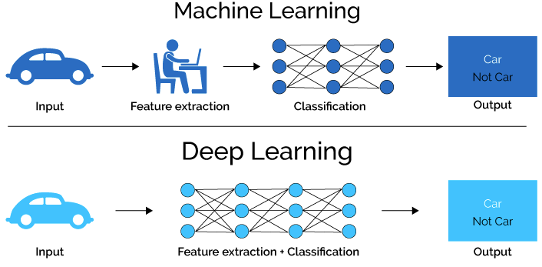Machine Learning vs Deep Learning
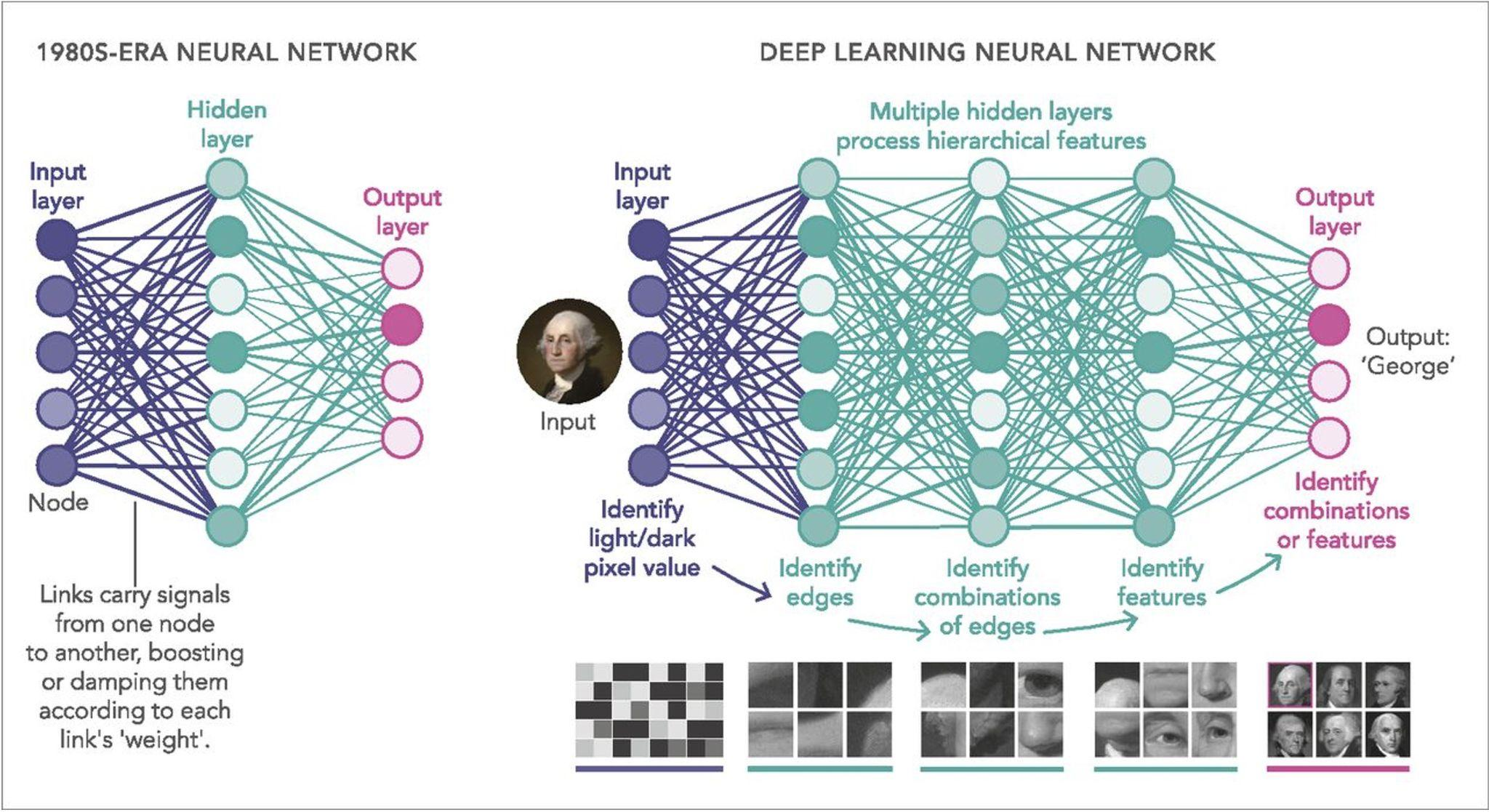Machine Learning vs Deep Learning
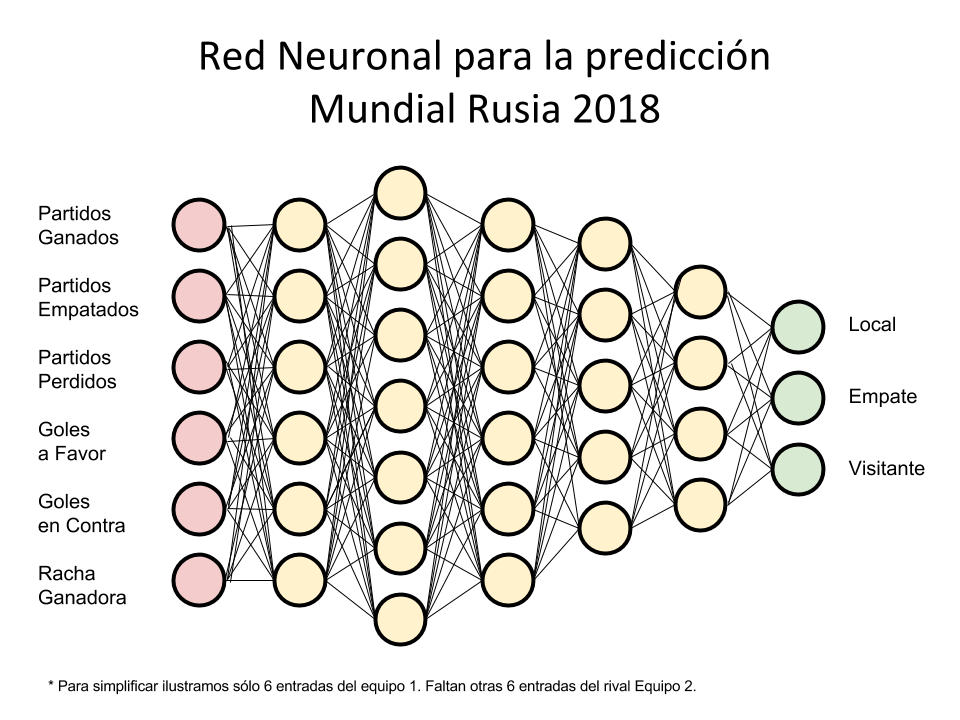Estimación del resultado de un partido de fútbol
¿Es lo mismo deep learning que aprendizaje profundo?
Si
Inconvenientes del Deep Learning
- El aprendizaje profundo “suele” requerir un conjunto de datos de gran tamaño para el entrenamiento.
- Los conjuntos de entrenamiento para el aprendizaje profundo se componen “a veces” de millones de puntos de datos.
- Una vez que se ha entrenado una red neuronal profunda con estos conjuntos de datos de gran tamaño, puede controlar más ambigüedad que una red superficial.
Topologías de Redes Neuronales Profundas
Existen muchas topologías de las redes neuronales:
- Red Neuronal de Avance - Feed Forward Neural Network (FFNN)
- Red de Base Radial - Radial Basis Network (RBN)
- Red de Alimentación Directa Profunda - Deep Feed Forward (DFF)
- Red con Memoria a Corto y Largo Plazo - Long / Short Term Memory (LSTM)
- Red de Unidades Periódicas Cerradas - Gated Recurrent Unit (GRU)
- Red Neuronal de Codificador Automático - Auto Encoder (AE)
- Red de Autoencoder Variacional - Variational Auto Encoder (VAE)
- Red de Codificador Automático de Eliminación de Ruido - Denoising Auto Encoder (DAE)
- Red de Autoencoder Dispersa - Sparse Auto Encoder (SAE)
- Red de Cadenas de Markov - Markov Chain (MC)
- Red Hopfield - Hopfield Network (HN)
- Red de Máquinas Boltzmann - Boltzmann Machine (BM)
- Red Restringida de Máquinas de Boltzmann - Restricted Boltzmann Machine (RBM)
- Red de Creencias Profundas - Deep Belief Network (DBN)
- Red Neuronal Convolucional - Convolutional Neural Network (CNN) o Deep Convolutional Network (DCN)
- Red Neuronal Deconvolucional - Deconvolutional Network (DN)
- Red de Gráficos Inversa Convolucional Profunda - Deep Convolutional Inverse Graphics - Network (DCIGN)
- Red Generativa de Adversarios - Generative Adversarial Network (GAN)
- Máquina de Estado Líquido - Liquid State Machine (LSM)
- Red de Máquinas de Aprendizaje Extremo - Extreme Learning Machine (ELM)
- Red de Estado de Eco - Echo State Network (ESN)
- Red Residual Profunda - Deep Residual Network (DRN)
- Red de Kohonen - Kohoner Network (KN)
- Máquina de Vector Soporte - Support Vector Machine (SVM)
- Máquina Neuronal de Turing - Neural Turing Machine (NTM)
Pero las más relevantes son:
- Feed Forward Neural Network (FFNN)
- Convolutional Neural Network (CNN) o Deep Convolutional Network (DCN)
- Recurrent Neural Network (RNN) o Long / Short Term Memory (LSTM)
- Generative Adversarial Network (GAN)
- Transformer Neural Networks
Feed Forward Neural Network (FFNN)
La forma más sencilla de estructurar una red neuronal. En Feed Forward Neural Network (FFNN) o red prealimentada, donde todas las neuronas de una capa se encuentran conectadas con todas las neuronas de la capa anterior. Cada conexión puede tener una fuerza o un peso diferente. En esta red, la información se mueve en una sola dirección, hacia adelante, desde los nodos de entrada, a través de los nodos ocultos y hacia los nodos de salida. No hay ciclos ni bucles en la red.
Cuando todas las neuronas de una capa están conectadas con todas las neuronas de la capa anterior, la capa se denomina completamente/densamente conectada.
Convolutional Neural Network (CNN o DCN)
- Las redes neuronales convolucionales (CNN) representan filtros anidados sobre datos organizados en cuadrículas. Son, con diferencia, el tipo de modelo más utilizado al procesar imágenes.
- Similares a las Densamente Conectadas.
- El modelo de redes neuronales convolucionales (CNN) se puede aplicar a tareas de reconocimiento visual.
- La arquitectura de una CNN está diseñada para aprovechar la estructura de matriz de los datos.
- Jerarquía de representaciones con creciente nivel de abstracción.
- Cada etapa es un tipo de transformación de característica entrenable. Por ejemplo, una primera capa convolucional aprende elementos básicos como aristas, y una segunda capa convolucional aprende patrones compuestos de elementos básicos aprendidos en la capa anterior. Y así sucesivamente en cada cada hasta ir aprendiendo patrones muy complejos.
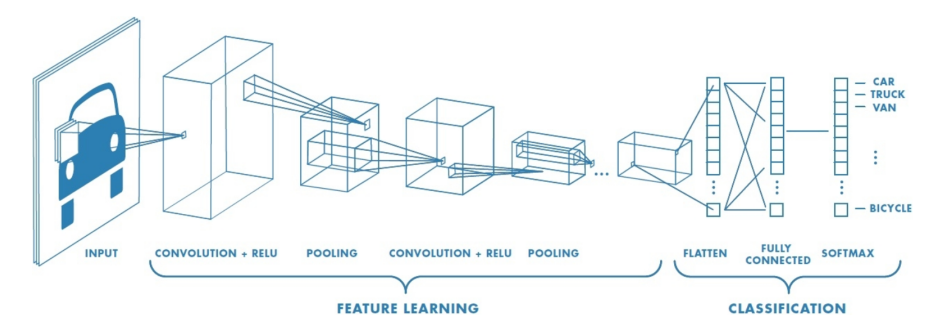Combinación de capas con diferentes tipos de redes neuronales convolucionales
Capa de convolución (Convolutional layer)
La diferencia fundamental entre una capa densamente conectada y una convolucional es que la capa densa aprende patrones globales en su espacio global de entrada, mientras que la capa convolucional aprende patrones locales dentro de la imagen en pequeñas ventanas de dos dimensiones.
Tomemos como referencia el caso del MNIST, dónde como entrada de nuestra red neuronal podemos pensar en un espacio de neuronas de dos dimensiones 28×28 (height=28, width=28, depth=1). Una primera capa de neuronas ocultas conectadas a las neuronas de la capa de entrada que hemos comentado realizarán las operaciones convolucionales que acabamos de describir. Pero no se conectan todas las neuronas de entrada con todas las neuronas de este primer nivel de neuronas ocultas, sino que solo se hace por pequeñas zonas localizadas del espacio de las neuronas de entrada que almacenan los píxeles de la imagen.
Si pensamos en una ventana del tamaño de 5×5, iremos recorriendo toda la capa de 28×28 de entrada que contiene la imagen. Esta ventana se va deslizando a lo largo de toda la capa de neuronas. Por cada posición de la ventana hay una neurona en la capa oculta que procesa esta información.
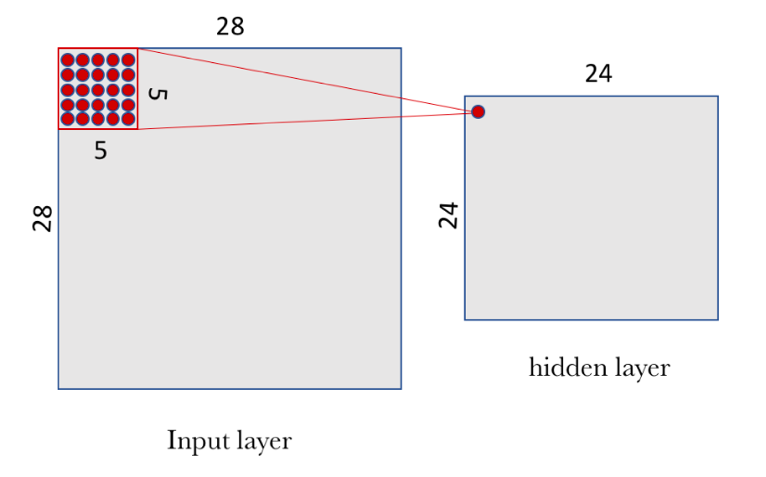Ventana de neuronas de la capa de entrada conectadas a neurona de la capa oculta convolucional
Visualmente, empezamos con la ventana en la esquina arriba-izquierda de la imagen, y esto le da la información necesaria a la primera neurona de la capa oculta. Después, deslizamos la ventana una posición hacia la derecha para “conectar” las 5×5 neuronas de la capa de entrada incluidas en esta ventana con la segunda neurona de la capa oculta. Y así, sucesivamente, vamos recorriendo todo el espacio de la capa de entrada, de izquierda a derecha y de arriba abajo.
Observemos que si tenemos una entrada de 28×28 píxeles y una ventana de 5×5 esto nos define un espacio de 24×24 neuronas en la primera capa del oculta, debido a que solo podemos mover la ventana 23 neuronas hacia la derecha y 23 hacia abajo antes de chocar con el lado derecho (o inferior) de la imagen de entrada.
En nuestro caso de estudio, y siguiendo el formalismo ya presentado previamente, para “conectar” cada neurona de la capa oculta con las 25 neuronas que le corresponden de la capa de entrada usaremos un valor de sesgo b y una matriz de pesos W de tamaño 5×5 que llamaremos filtro (o kernel/filter en inglés).
En la siguiente imagen, vemos otro ejemplo partiendo de una capa de entrada de 49 neuronas (imagen de 7x7) y un filtro con ventana de 3x3, generará una capa oculta resultante de 25 neuronas (matriz de 5x5) con un padding de relleno a ceros alrededor del margen de la imagen (mejora el resultado del barrido que se realiza en la ventana que se va deslizando)
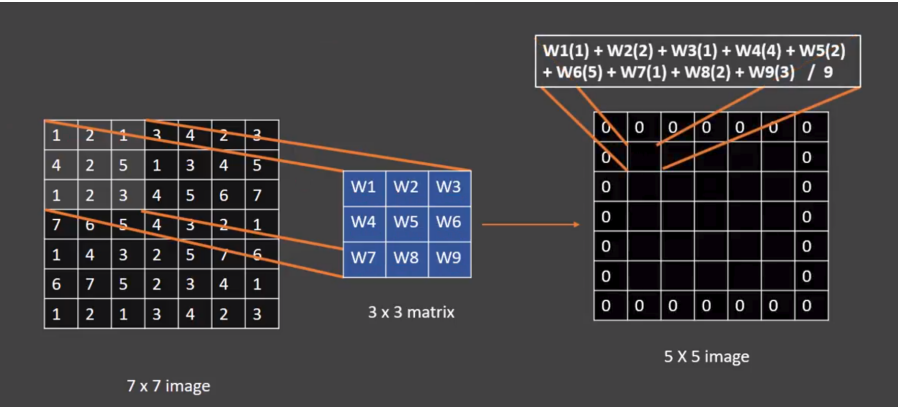Capa convolucional con ventana de 3x3
Es muy importante tener en cuenta que en las redes convolucionales se usa el mismo filtro (la misma matriz W de pesos y el mismo sesgo b) para todas las neuronas de la capa oculta.
Pero un filtro definido por una matriz W y un sesgo b solo permiten detectar una característica concreta en una imagen; por tanto, para poder realizar el reconocimiento de imágenes se propone usar varios filtros a la vez, uno para cada característica que queramos detectar. En el siguiente ejemplo, vemos que se aplican 32 filtros, donde cada filtro recordemos que se define con una matriz W de pesos compartida de 5×5 y un sesgo b.
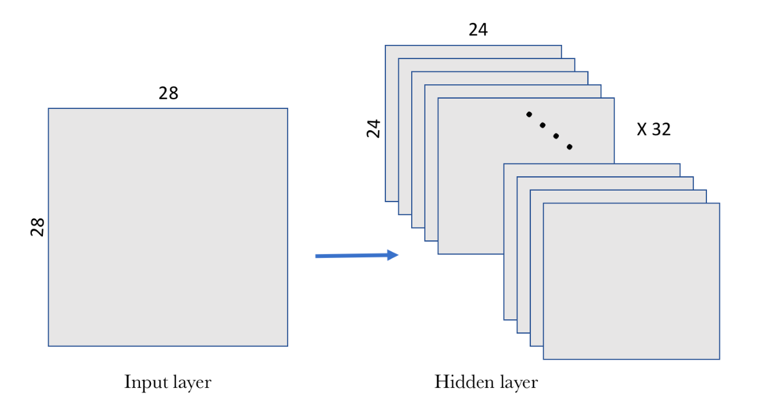Capa oculta convolucional con 32 filtros
Capa de pooling (Pooling layer)
Además de las capas convolucionales que acabamos de describir, las redes neuronales convolucionales acompañan a la capa de convolución con unas capas de pooling, que suelen ser aplicadas inmediatamente después de las capas convolucionales. Su función es reducir progresivamente el tamaño espacial de la representación para reducir la cantidad de parámetros y computación en la red. La capa de agrupación opera en cada mapa de características de forma independiente.
Hay varias maneras de condensar la información, pero una habitual, y que usaremos en nuestro ejemplo, es la conocida como max-pooling, . En el siguiente ejemplo, vemos que se define una ventana de entrada de 2x2 y se queda con el valor máximo de los existentes en la ventana. De esta forma, dividimos por 4 el tamaño de la salida de la capa de pooling, quedando una imagen de 12×12.
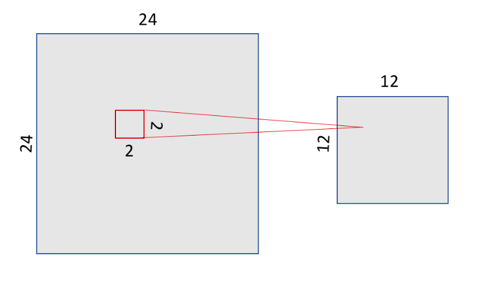Capa de pooling con ventana de 2x2
En la siguiente captura tenemos una captura de una imagen 7x7 donde se le aplica una ventana 2x2 con un stride (longitud del paso de avance) de 2 en lugar de 1 y por tanto obtenemos un mapa de caracteres de 4x4
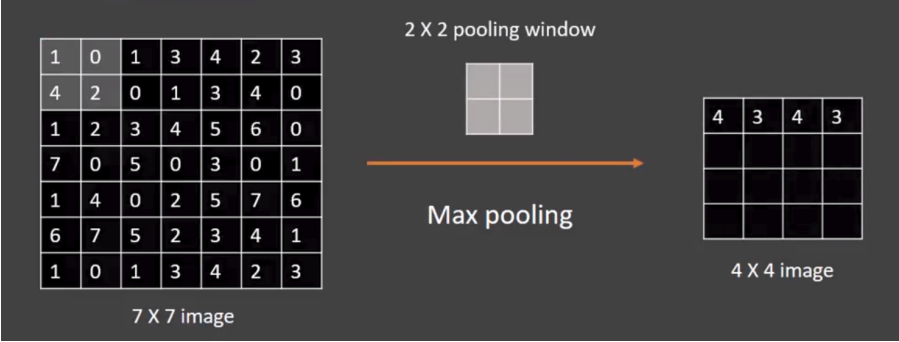Capa de pooling con ventana 2x2 con stride de 2
¿Qué es el stride?
En la siguiente imagen, vemos gráficamente el resultado de combinar la convolución con pooling:
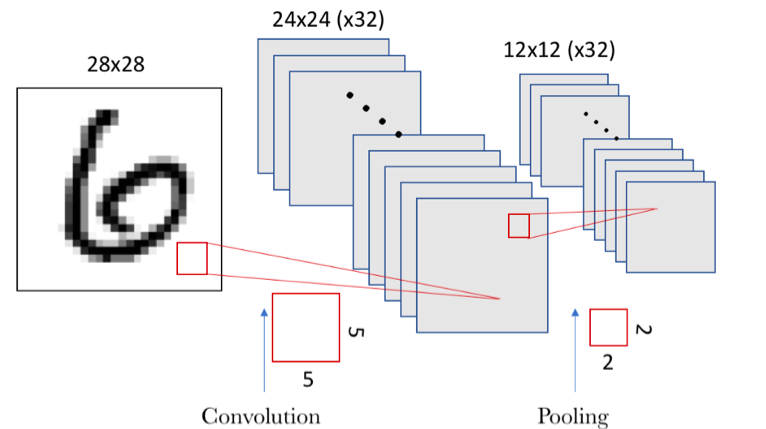Combinación de capa de convolución con capa de pooling
¿Se pueden combinar las capas de convolución y capas de pooling?
Recurrent Neural Network (RNN) o Long / Short Term Memory (LSTM)
Las redes neuronales recurrentes (RNN) y los tipos de modelos de memoria a corto plazo a largo plazo (LSTM) están estructurados para representar de manera efectiva los bucles for en la computación tradicional, recolectando estados mientras se itera sobre algún objeto. Por tanto, en este tipo de redes la información puede fluir en cualquier dirección. Se pueden utilizar para procesar secuencias de datos.
Limitación con Feed Forward Neural Networks (y CNN):
- No diseñadas para datos secuenciales.
- Dimensión fija de entradas.
- No modela la memoria.
Las redes neuronales recurrentes permiten:
- Para mapear predicciones en secuencias.
- Esto crea un estado interno de la red que le permite exhibir relaciones temporales dinámicas.
- Aplicaciones: subtítulos de imágenes, análisis de sentimientos, respuesta a preguntas, reconocimiento de voz, series temporales, generación de música, traducción automática, vehículos autónomos, …
Transformer Neural Networks
Un reemplazo más moderno para los RNN/LSTM, la arquitectura del transformador permite el entrenamiento sobre conjuntos de datos más grandes que involucran secuencias de datos.
Generative Adversarial Network (GAN)
¿Qué es Generative AI?
La IA generativa es uno de los mayores avances recientes en IA debido a su capacidad para crear nuevas cosas. Hasta hace poco, la mayoría de las aplicaciones de aprendizaje automático funcionaban con modelos discriminativos.
Un modelo discriminativo tiene como objetivo responder la pregunta: “Si estoy mirando algunos datos, ¿cómo puedo clasificar mejor estos datos o predecir un valor?” Por ejemplo, podríamos usar modelos discriminativos para detectar si una cámara apunta a un gato. Mientras entrenamos este modelo sobre una colección de imágenes (algunas de las cuales contienen gatos y otras que no), esperamos que el modelo encuentre patrones en las imágenes que ayuden a hacer esta predicción.
Un modelo generativo tiene como objetivo responder a la pregunta: “¿He visto datos como este antes?” En nuestro ejemplo de clasificación de imágenes, aún podríamos usar un modelo generativo al enmarcar el problema en términos de si una imagen con la etiqueta “gato” es más similar a los datos que ha visto antes que una imagen con la etiqueta “sin gato”.
Sin embargo, los modelos generativos se pueden utilizar para respaldar un segundo caso de uso. Los patrones aprendidos en modelos generativos se pueden utilizar para crear nuevos ejemplos de datos que se parecen a los datos que se vieron antes.
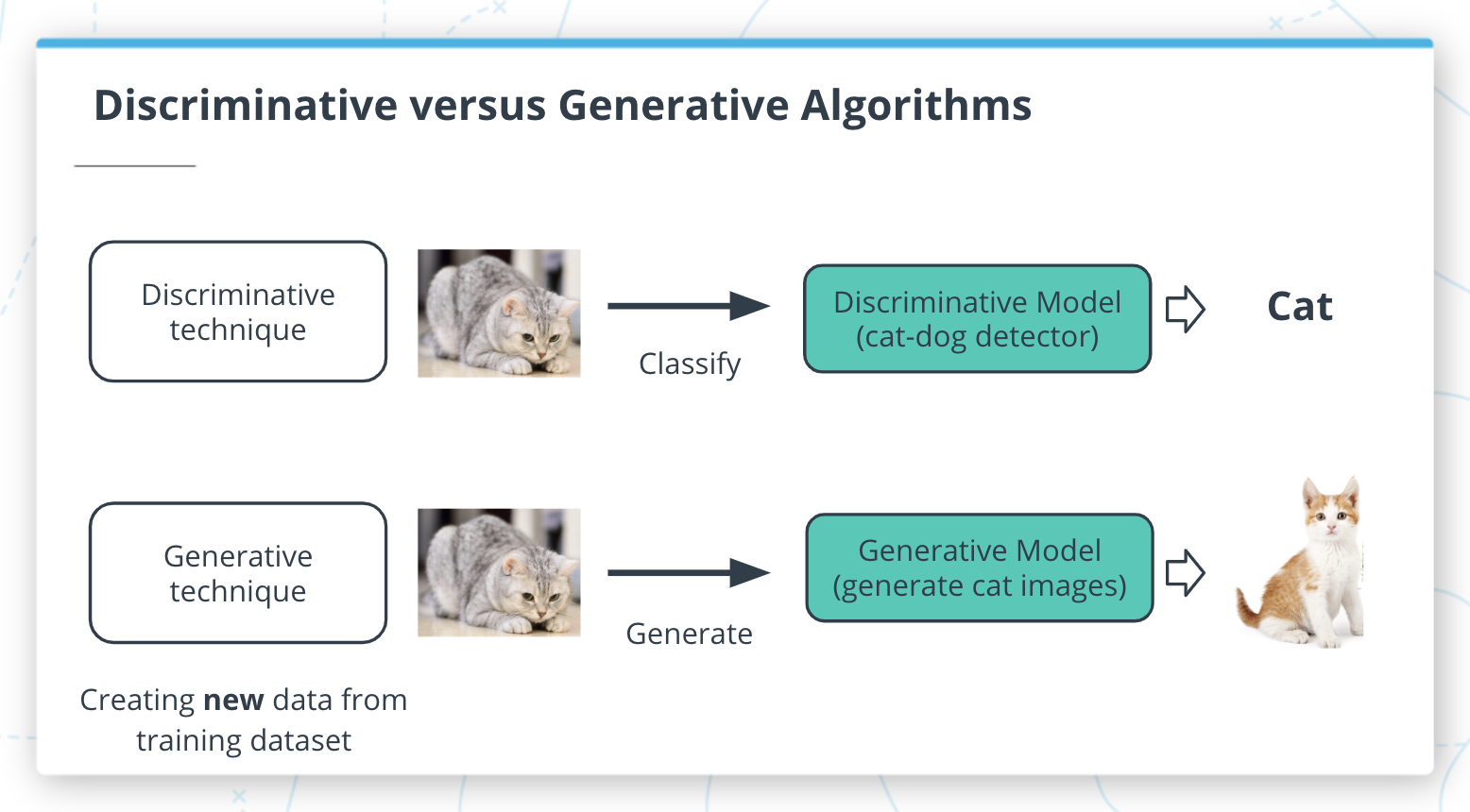Algoritmos discriminativos vs algoritmos generativos
Las redes generativas adversarias (GAN) son un formato de modelo de aprendizaje automático que implica enfrentar dos redes entre sí para generar contenido nuevo. El algoritmo de entrenamiento alterna entre entrenar una red de generador (responsable de producir nuevos datos) y una red discriminadora (responsable de medir qué tan cerca los datos de la red del generador representan el conjunto de datos de entrenamiento).
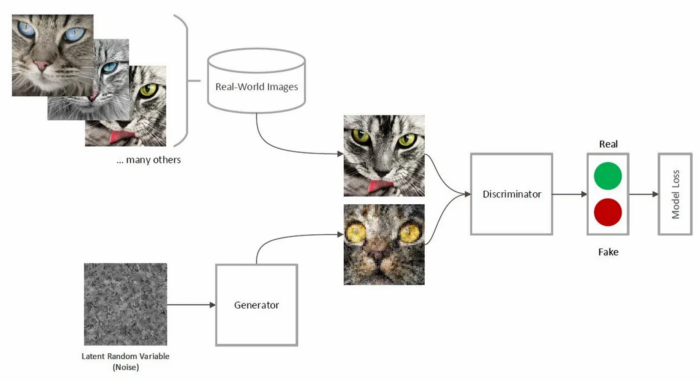Ejemplo GAN
¿Cómo funcionan los filtros de FaceApp?
Documental sobre Machine Learning y Entrenamiento Humano: https://www.documaniatv.com/social/trabajadores-fantasma-video_bd817bfb9.html.
Fases del entrenamiento de una Red Neuronal Profunda
Descarga los ejemplos: demoKeras1.ipynb, demoKeras2.ipnyb
Etapas para crear una RN densamente conectada:
Etapa 1:
Creación del modelo y definición de cada una de las capas.
model = new Sequential()model.add(Dense(<número de neuronas>, activation=<función de activación (‘sigmoid’, ‘softmax’, ‘relu’...)>)
Etapa 2:
Configuración del proceso de aprendizaje: método compile:
- función de coste (
loss function): evalúa el grado de error entre las salidas calculadas y las salidas deseadas de los datos de entrenamiento. El objetivo está en reducir dicho valor en cada iteración. - optimizador (
optimizer): es la manera que tenemos de indicar los detalles del algoritmo de optimización que permite a la red neuronal calcular los pesos de los parámetros durante el entrenamiento a partir de los datos de entrada y de la función de coste definida. - métrica (
metrics): es la que usaremos para monitorizar el proceso de aprendizaje y prueba de nuestra red neuronal. Si indicamosaccuracysolo tendremos en cuenta la fracción de datos que son correctamente clasificados, es decir, la proporción entre las predicciones correctas que ha hecho el modelo del total de predicciones.
Etapa 3:
Entrenamiento con los datos de training: método fit:
epochs: número de veces que usaremos todos los datos en el proceso de aprendizaje.verbose: permite ver el avance del entrenamiento así como una estimación de cuánto tarda cada época.
Etapa 4:
Evaluación con los datos de testing: método evaluate:
Para redes neuronales que clasifiquen, volveremos a referirnos a la matriz de confusión:
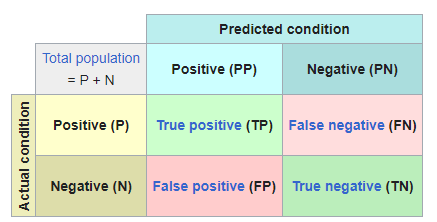Método evaluate
- TP: cantidad de positivos que fueron clasificados correctamente como positivos por el modelo.
- TN: cantidad de negativos que fueron clasificados correctamente como negativos por el modelo.
- FN: cantidad de positivos que fueron clasificados incorrectamente como negativos.
FP: cantidad de negativos que fueron clasificados incorrectamente como positivos.
- Si utilizamos la precisión (accuracy), conoceremos la proporción entre las predicciones correctas que ha hecho el modelo del total de predicciones, ya que
Presicion=(TP+TN)/(TP+TN+FP+FN). - Si utilizamos el recall: sabremos como de bien el modelo evita los falsos negativos, ya que Recall = TP/(TP+FN)
Etapa 5:
Generación de predicciones: método predict.
Función de pérdida (Loss function)
En las redes neuronales, las funciones de pérdida ayudan a optimizar el rendimiento del modelo. Suelen utilizarse para medir alguna penalización en la que incurre el modelo en sus predicciones, como la desviación de la predicción con respecto a la etiqueta de verdad. Las funciones de pérdida suelen ser diferenciables en todo su dominio (pero se permite que el gradiente sea indefinido sólo para puntos muy concretos, como x = 0, que básicamente se ignora en la práctica). En el bucle de entrenamiento, se diferencian con respecto a los parámetros, y estos gradientes se utilizan para sus pasos de retropropagación y descenso de gradiente para optimizar su modelo en el conjunto de entrenamiento.
Las funciones de pérdida también son ligeramente diferentes de las métricas. Mientras que las funciones de pérdida pueden indicarnos el rendimiento de nuestro modelo, puede que no sean de interés directo o fácilmente explicables por los humanos. Aquí es donde entran en juego las métricas. Métricas como la precisión son mucho más útiles para que los humanos entiendan el rendimiento de una red neuronal, aunque no sean buenas opciones para las funciones de pérdida, ya que pueden no ser diferenciables.
Existen diferentes métricas del error según trabajamos con problemas de regresión o clasificación.
Métricas para problemas de regresión y RRNN:
- The Mean Absolute Error (Error absoluto medio): $EAM = \frac{1}{n} \sum_{i=1}^{n} abs(y_i - \hat{y}_i)$
- Mean Squared Error (Error cuadrático medio): $ECM = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$
- Raíz Cuadrada del Error Cuadrático Medio $RCECM = \frac{1}{n} \sum_{i=1}^{n} \sqrt{(y_i - \hat{y}_i)^2}$
- Logarithmic Loss: $LogLoss = -\frac{1}{n} \sum_{i=1}^{n} [y_i \log(\hat{y}_i) + (1-y_i) \log(1-\hat{y}_i)]$
- Accuracy
Métricas para regresiones logísticas cuando tenemos dos clasificaciones:
- Logistic Loss
- Binary Cross Entropy (Entropía cruzada binaria)
Métricas para problemas de clasificación:
- Categorical Cross Entropy (Entropía Cruzada Categórica): Esta función necesita que la salida de la red neuronal sean tantos nodos como categorías hay.
- Sparse Categorical Cross Entropy (Entropía Cruzada Categórica Dispersa)
Descenso del gradiente
El descenso de gradiente es un algoritmo de optimización de primer orden.
Encuentre un mínimo local de una función usando el descenso de gradiente, uno da pasos proporcionales al negativo del gradiente de la función en el punto actual.
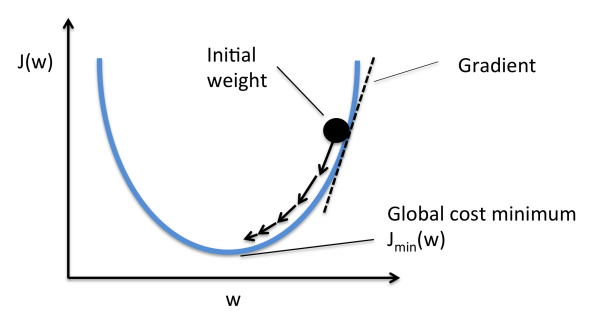Ilustración del descenso de gradiente en una serie de conjuntos de niveles
La función de pérdida toma las predicciones de la red y las compara con los targets objetivo. De esta forma, calcula una puntuación de distancia, capturando cómo de bien funciona la red neuronal.
El truco fundamental en el aprendizaje profundo es utilizar esta puntuación como una señal de retroalimentación para ajustar un poco el valor de los pesos, en una dirección que reducirá la puntuación de pérdida para el lote actual de ejemplos (gradiente negativo).
El gradiente ($\nabla J (\theta)$) se calcula por retropropagación.
Calcula el gradiente de una función de pérdida con respecto a todos los pesos en la red (regla de la cadena) y lo usa para actualizar los pesos para minimizar la función de pérdida.