Tabla de contenidos
1. Introducción
Pruebas… ¿para qué?
- Detectar errores.
- Analizar el rendimiento o carga de CPU.
- Evitar problemas en producción graves. ¿Qué es un problema grave?
- Aumentar la fiabilidad y robustez de un software.
- Generar seguridad cuando tocamos ciertas partes del código.
¿Las pruebas aumentan el coste en la creación de un software?
2. Tipos de pruebas
- Pruebas de caja blanca
- Pruebas de caja negra
2.1. Pruebas de caja blanca
Mediante esta técnica se pretenden obtener casos de prueba que:
- Garanticen que se ejecutan al menos una vez todos los caminos independientes.
- Ejecuten todas las sentencias al menos una vez.
- Ejecuten todas las decisiones lógicas en su parte verdadera y falsa.
- Ejecuten todos los bucles en sus límites.
- Utilicen todas las estructuras de datos internas para asegurar su validez.
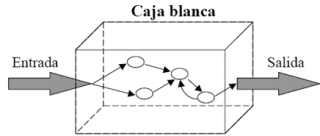Caja blanca
Se basan en el minucioso examen de los detalles procedimentales del código de la aplicación.
Una de las técnicas utilizadas para desarrollar los casos de prueba de caja blanca es la prueba del camino básico.
2.2. Pruebas de caja negra o de comportamiento
Estas pruebas se llevan a cabo sobre la interfaz del software, no hace falta conocer la estructura interna del programa ni su funcionamiento.
Se pretende obtener casos de prueba que demuestren que las funciones del software son operativas, es decir, que las salidas que devuelve la aplicación son las esperadas en función de las entradas que se proporcionen.
Caja negra
3. Estrategia de las pruebas de software
- Pruebas de unidad o unitarias
- Pruebas de integración
- Pruebas de validación
- Pruebas de sistema
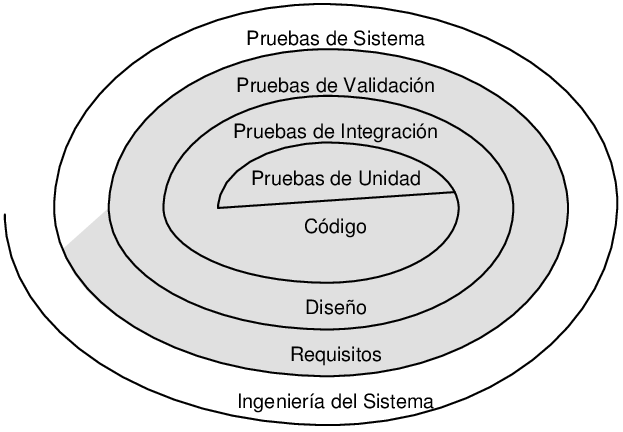Estrategia de las pruebas de software
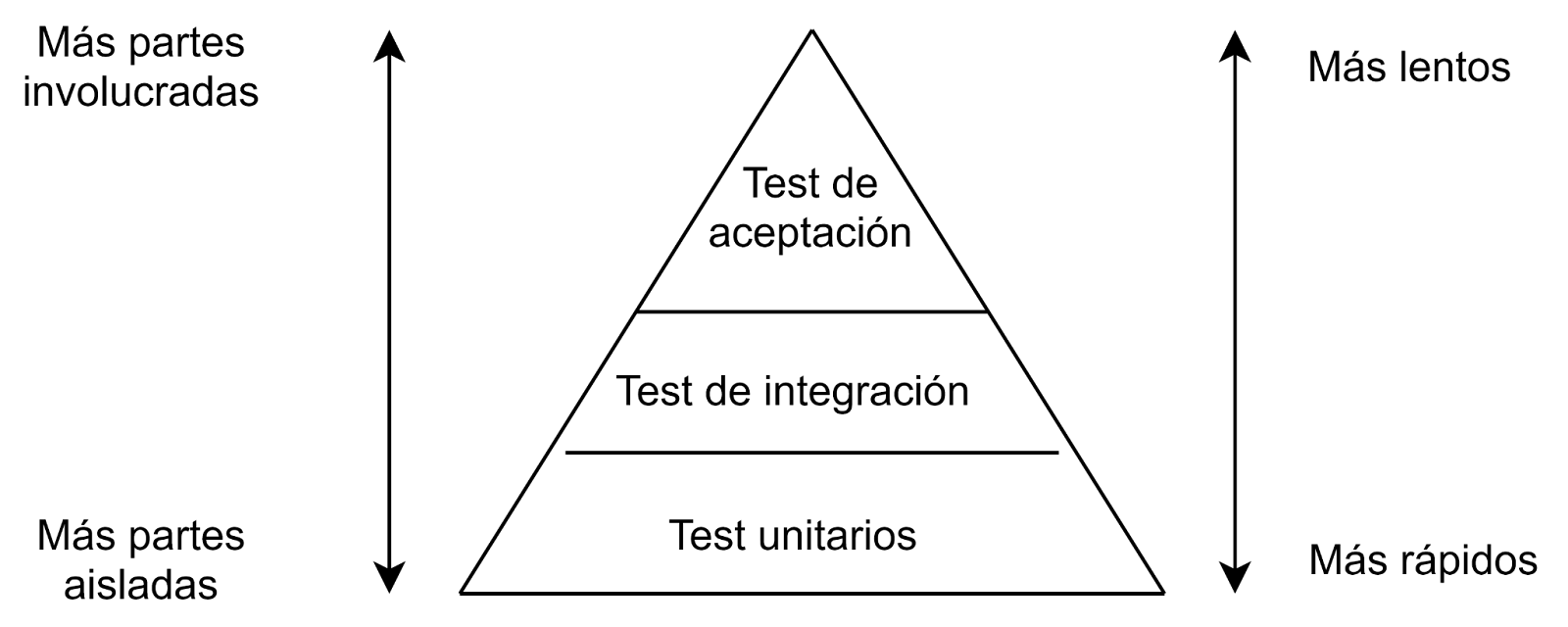Pirámide de las estrategias de software
3.1. Pruebas de unidad o unitarias
En este nivel se prueba cada unidad o módulo con el objetivo de eliminar errores en la lógica interna. Esta estrategia utiliza técnicas de caja negra y caja blanca, según convenga para lo que se desea probar. Las pruebas unitarias deben cumplir con las siguientes características:
- Debe ser un bloque básico de construcción de programas.
- Debe implementar una función independiente simple.
- Podrá ser probado al cien por cien por separado.
- No deberá tener más de 500 líneas de código.
3.2. Pruebas de integración
En este tipo de pruebas se observa cómo interaccionan los distintos módulos. Se podría pensar que esta prueba no es necesaria ya que si dos módulos funcionan por separado, deberían funcionar juntos, pero la realidad no es tan simple.
Hay dos enfoques para la realización de estas pruebas:
- Integración no incremental.
- Integración incremental.
3.3. Pruebas de validación
En este tipo de pruebas se comprueba si el software funciona de acuerdo a las expectativas del cliente. Estas expectativas suelen estar definidas en un documento de los requisitos del software. Las técnicas a utilizar son:
- Prueba Alfa: Se lleva a cabo por el cliente o el desarrollador.
- Prueba Beta: Se lleva a cabo por los usuarios finales.
3.4. Pruebas de sistema
En este tipo de pruebas se busca poner al límite el software para comprobar su comportamiento. Son las siguientes:
- Pruebas de recuperación
- Pruebas de seguridad
- Pruebas de resistencia o stress.
4. Prueba del camino/ruta básico
Es una técnica de prueba de caja blanca que permite al diseñador de casos de prueba obtener una medida de complejidad lógica de un diseño procedimental y usar esa medida como guía para la definición de un conjunto básico de caminos de ejecución.
Caja blanca
Los casos de prueba obtenidos del conjunto básico garantizan que durante la prueba se ejecuta por lo menos una vez cada sentencia del programa.
Para la obtención de la medida de la complejidad lógica emplearemos una representación de flujo de control denominada “grafo de flujo” o “grafo del programa”.
4.1. Pasos para la prueba del camino/ruta básico
- Dibujar el grafo de flujo.
- Complejidad ciclomática.
- Obtención de los casos de prueba.
4.1.1. Dibujar el grafo de flujo
Cada círculo del grafo se llama nodo. Cada nodo representa una o más sentencias que no tienen bifurcaciones.
Las flechas del grafo de flujo se denominan aristas o enlaces y representan el flujo de control.
Las áreas delimitadas por aristas y nodos se denominan regiones, siendo el área exterior del grafo una región más.
4.1.2. Complejidad ciclomática
La complejidad ciclomática es una técnica de software que proporciona una medida cuantitativa de la complejidad lógica de un programa.
En este contexto, la complejidad ciclomática establece el número de caminos independientes del conjunto básico de caminos de ejecución de un programa.
La complejidad ciclomática se calcula de 3 formas:
- V(G) = Número de regiones de un grafo
- V(G) = Aristas - Nodos + 2
- V(G) = Nodos predicado + 1
4.1.3. Obtención de caminos independientes
En este método se elige el primer camino como uno que cumpla todas las condiciones con TRUE. A partir del camino inicial se va variando hasta completar los caminos necesarios. El procedimiento se puede describir de la siguiente manera:
- Asegurarse que solo hay un nodo final y uno inicial
- Seleccionar el camino feliz o happy path.
- Mientras no existan nodos de decisión con salidas no utilizadas y el número de caminos sea < V(G):
- Seguir el camino feliz hasta el primer nodo predicado que no hayamos explorado sus dos opciones.
- Buscar regresar al camino básico tan pronto como sea posible.
4.1.4. Obtención de los casos de prueba
El último paso de la prueba del camino básico es construir los casos de prueba que fuerzan la ejecución de cada camino.
4.2. Ejemplo prueba del camino/ruta básico
Este diagrama flujo corresponde al algoritmo para determinar el número mayor de 3 valores dados.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
* Devuelve el número mayor de entre a, b y c
*/
public static int determinaMayor(int a, int b, int c) {
if (a > b && a > c) {
return a;
} else {
if (c > b) {
return c;
} else {
return b;
}
}
}
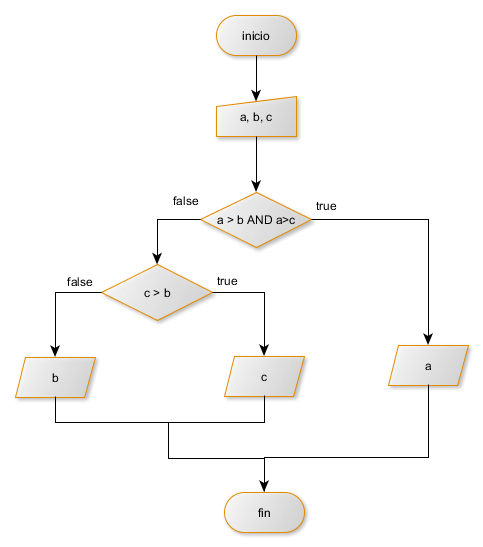Diagrama de flujo
4.2.1. Dibujar el grafo de flujo
Detectamos los nodos que conformarán el grafo de flujo así como los caminos que se pueden recorrer durante la ejecución del programa.
Si tenemos una condición compuesta, como es nuestro caso (a>b AND a>c), debemos descomponerla creando un nodo para cada una de las condiciones.
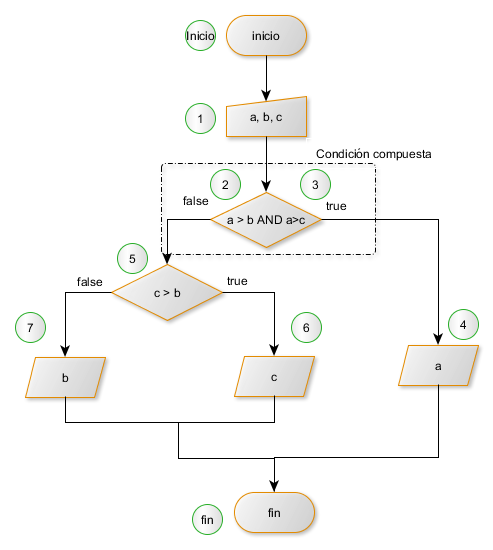Diagrama de flujo con números
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
* Devuelve el número mayor de entre a, b y c
*/
public static int determinaMayor(int a, int b, int c) {
// 1
if (a > b && a > c) { // 2 y 3
return a; // 4
} else {
if (c > b) { // 5
return c; // 6
} else {
return b; // 7
}
}
// F
}
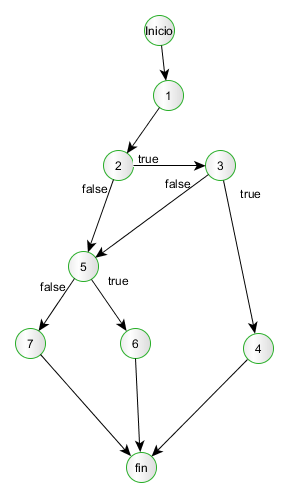Grafo de flujo
4.2.2. Complejidad ciclomática
La complejidad ciclomática mide el número de caminos independientes dentro de nuestro código que es sometido a prueba. La fórmula para su cálculo es:
V(G) = Aristas - Nodos + 2
En nuestro ejemplo la fórmula queda de la siguiente forma:
V(G) = 11 – 9 + 2 = 4
4.2.3. Caminos independientes
| Camino | Entrada | Prueba | Salida |
|---|---|---|---|
| 1,2,3,5,6,F | a>b=TRUE, a>c=FALSE, c>b=TRUE | a=6, b=3, c=7 | 7 |
| 1,2,3,4,F | a>b=TRUE, a>c=TRUE | a=5, b=3, c=4 | 5 |
| 1,2,5,7,F | a>b=FALSE, a>c=FALSE | a=5, b=7, c=6 | 7 |
| 1,2,5,6,F | a>b=FALSE, a>c=TRUE | a=5, b=7, c=4 | 9 |
5. Partición o clases de equivalencia
La partición equivalente es un método de prueba de caja negra que divide los valores de los campos de entrada de un programa en clases de equivalencia.
Para identificar las clases de equivalencia se examina cada condición de entrada y se divide en dos o más grupos. Hay dos tipos de clases de equivalencia:
- Clases válidas: son valores de entrada válidos.
- Clases no válidas: son los valores de entrada no válidos.
Caja negra
5.1. Ejemplo 1
Supongamos un campo de entrada llamado numEmpleado, definido con una serie de condiciones: numérico de 3 dígitos y el primero no puede ser 0.
Entonces se pueden definir dos clases de equivalencia:
- Una no válida: numEmpleado < 100
- Otra no válida: numEmpleado > 999
- Otra válida: numEmpleado comprendido entre 100 y 999.
5.2. Clases de equivalencia
Las clases de equivalencia se definen según una serie de directrices. Si una condición de entrada…
- Especifica un rango…
- 1 clase de equivalencia válida
- 2 clases de equivalencia no válidas
- Requiere un valor específico…
- 1 clase de equivalencia válida
- 2 clase de equivalencia no válida
- Especifica un miembro de un conjunto…
- 1 clase de equivalencia válida
- 1 clase de equivalencia no válida
- Es lógica…
- 1 clase de equivalencia válida
- 1 clase de equivalencia no válida
5.3. Ejemplo 2
Se va a realizar una entrada de datos de un empleado por pantalla gráfica, se definen 3 campos de entrada y una lista para elegir el oficio. La aplicación acepta los datos de esta manera:
- Empleado: número de tres dígitos que no empiece por 0.
- Departamento: en blanco o número de dos dígitos.
- Oficio: Analista, Diseñador, Programador.
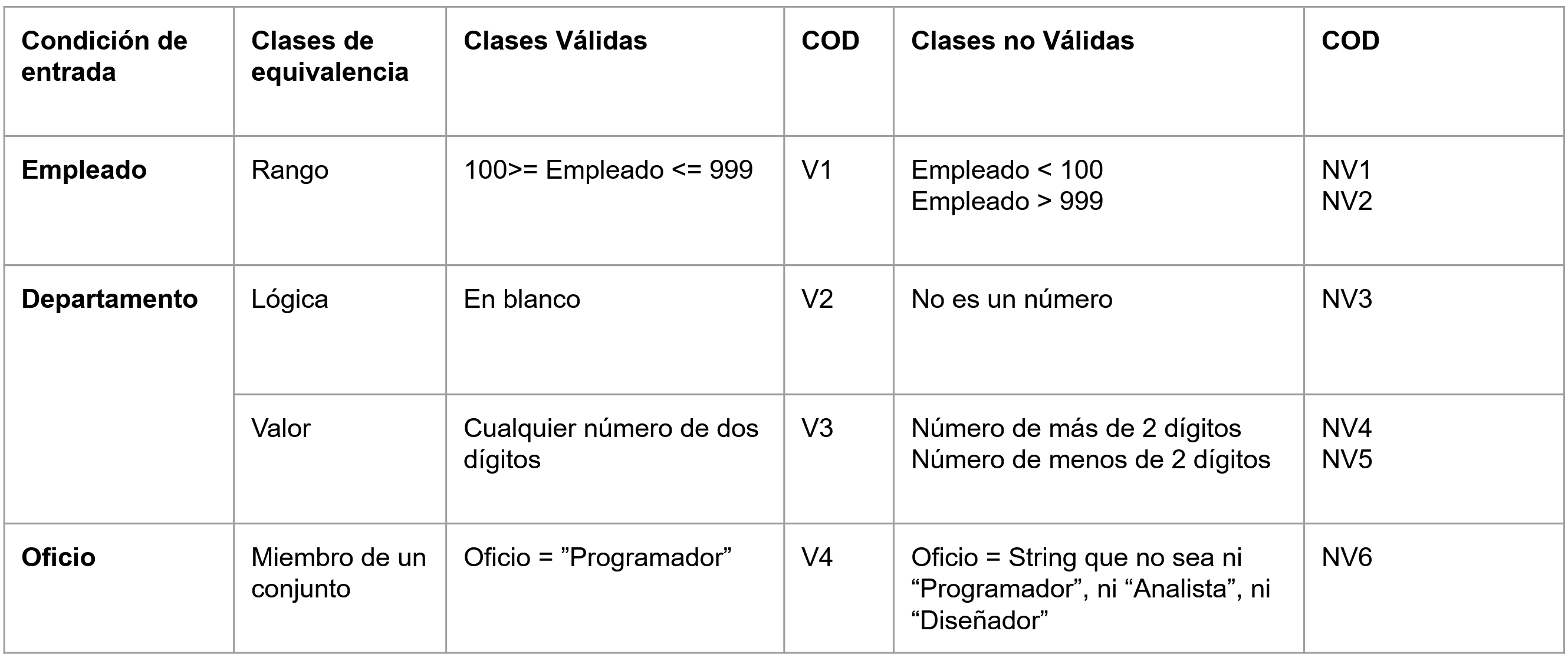Tabla de clases de equivalencia
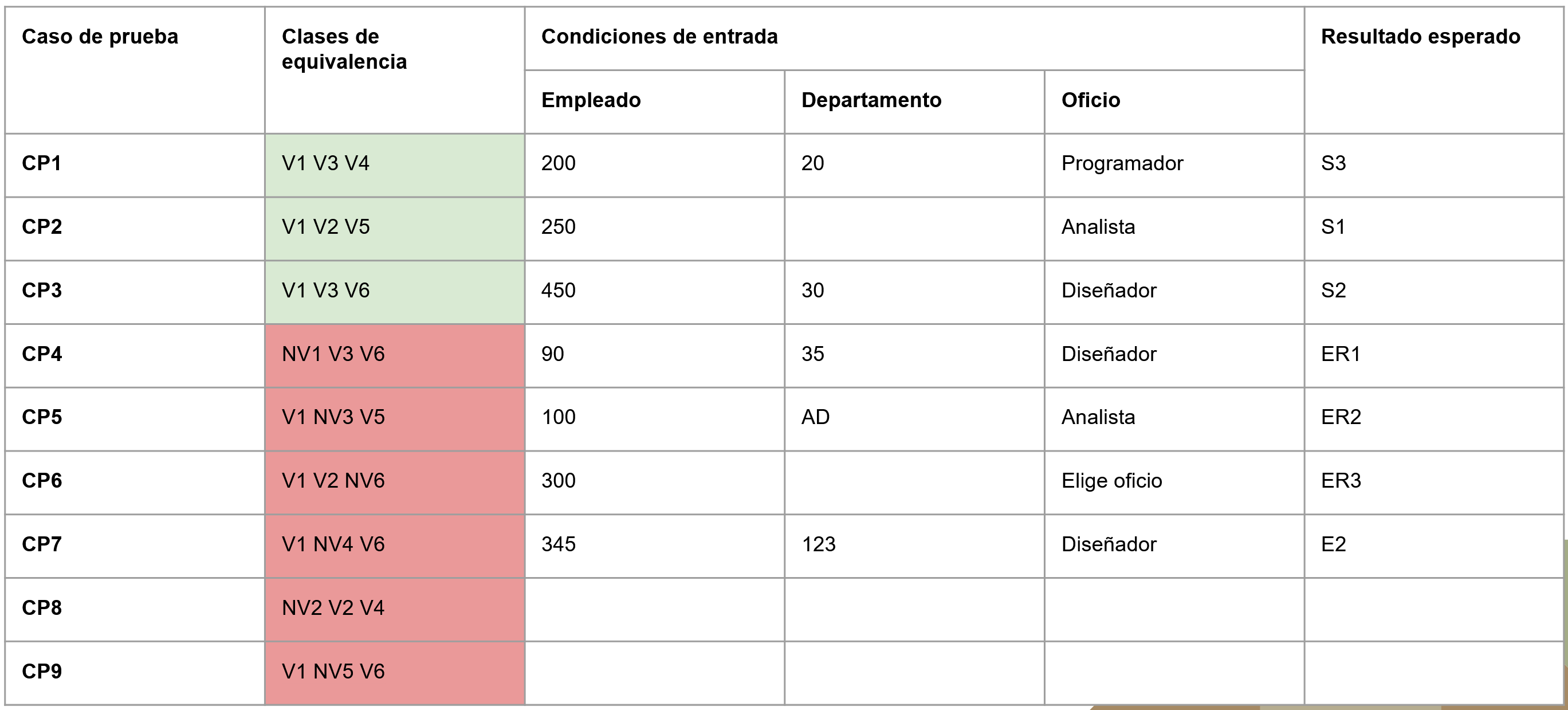Casos de prueba
6. Análisis de Valores Límite
El análisis de valores límite se basa en que los errores tienden a producirse con más probabilidad en los límites o extremos de los campos de entrada.
Esta técnica complementa a la anterior y los casos de prueba elegidos ejercitan los valores justo por encima y por debajo de los márgenes de la clase de equivalencia. Además se exploran las condiciones de salida definiendo las clases de equivalencia de salida.
6.1. Reglas de AVL
- Si tenemos un rango de valores de entrada, se deben diseñar:
- 2 casos de prueba válidos
- 2 casos de prueba no válidos
- Si tenemos un rango de valores de salida, se deben diseñar:
- 2 casos de prueba válidos
- 2 casos de prueba inválidos (si es posible)
- Si las estructuras de datos internas tienen límites pre-establecidos, por ejemplo un array de 100 elementos, hay que asegurarse de diseñar casos de prueba que pruebe la estructura en sus límites.
6.2. Ejemplo 2
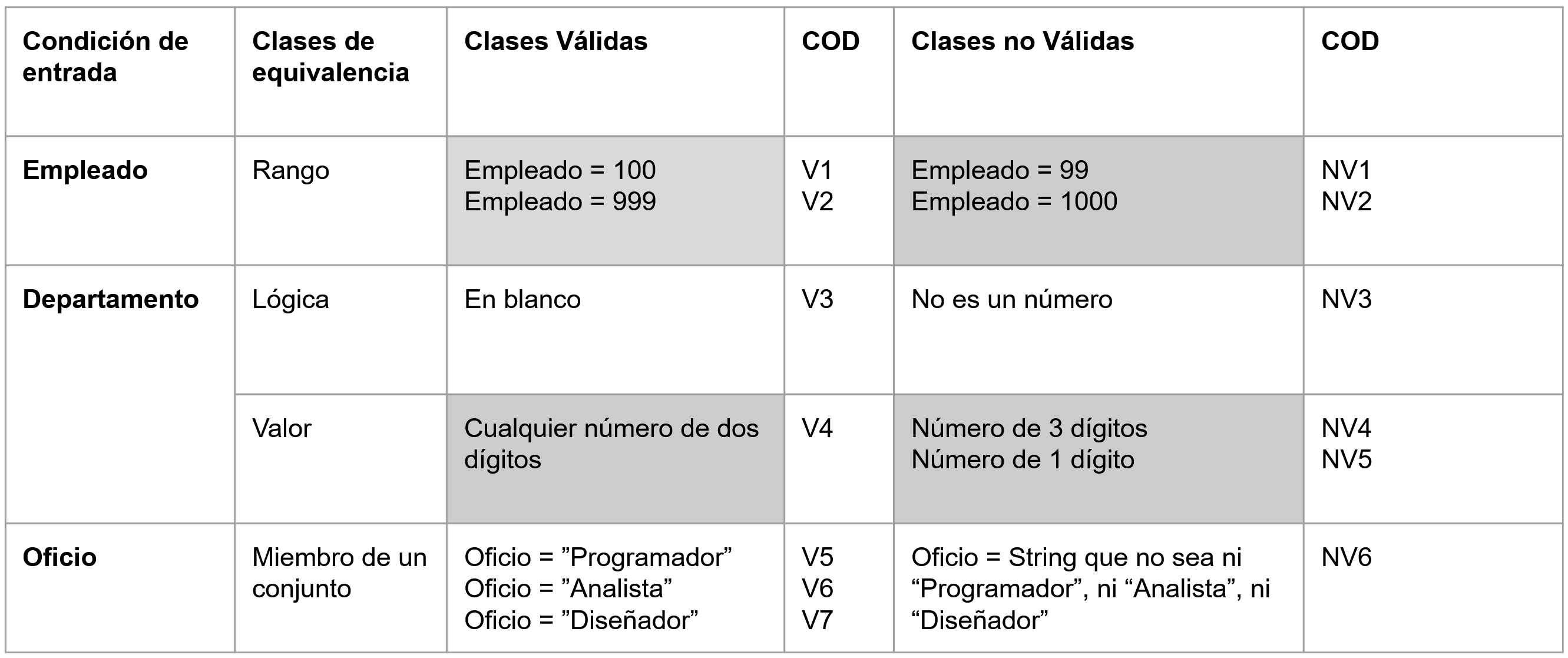Tabla de clases de equivalencia con valores límite
7. Pruebas con JUnit
JUnit es una librería (fichero .jar) escrita en Java para la realización de test unitarios.
Las etiquetas JUnit más usadas son las siguientes:
@Test: El método que tenga esta etiqueta será un test.@BeforeAll: Este método se ejecutará antes del primer test.@AfterAll: Este método se ejecutará después del último test.@BeforeEach: Este método se ejecutará antes de cada test.@AfterEach: Este método se ejecutará después de cada test.