Aprendizaje Supervisado

Introducción

El aprendizaje supervisado se basa en modelos predictivos que hacen uso de datos de entrenamiento. El modelo se entrena con un juego de datos que incluye variables (features) y resultados (labels). Se busca que el modelo sea capaz de generalizar.

El aprendizaje supervisado se puede subdividir según la funcionalidad buscada:

• Clasificación. Puede ser binaria o multiclase. En el primer caso, se trata de una decisión binaria (Sí/No) y se clasifica entre dos clases. En el segundo caso, clasifica entre más de dos clases. En otras palabras, estamos tratando de mapear variables de entrada en categorías discretas.
• Regresión. Cálculo de un valor determinado. Es decir, estamos tratando de predecir resultados dentro de una salida continua, lo que significa que estamos tratando de asignar variables de entrada a alguna función continua.

Imaginemos un supuesto donde disponemos de un dataset sobre viviendas en el mercado inmobiliario. Si intentamos predecir el precio en función del tamaño es una salida continua, por lo que es un problema de regresión. Podríamos convertir el mismo supuesto en un problema de clasificación considerando obtener “todas las viviendas en venta por encima o por debajo de un determinado precio de venta”. En este caso, se clasifican las viviendas según su precio en dos categorías discretas.

Otros ejemplos:

• Regresión: dada una imagen de una persona, tenemos que predecir su edad en base a una imagen facilitada; calcular precios de productos, de viviendas…
• Clasificación: dado un paciente con un tumor, predecir si el tumor es maligno o benigno; calcular el impago/pago de un crédito…

¿Cuál es la diferencia entre clasificación y regresión?

Casos de aprendizaje supervisado son:

• KNN (K-Nearest Neighbours)
• Regresión Lineal
• Regresión Logística
• Árboles de decisión
• Máquinas de Vector Soporte (SVM)

Pero antes de verlos debemos preprocesar los datos.

Preprocesamiento de los datos

Preprocesamiento de los datos

KNN (K-Nearest Neighbours)

KNN

Regresión Lineal

Los modelos lineales simplemente describen la relación entre un conjunto de números de entrada y un conjunto de números de salida a través de una función lineal $y = b0+ b1x$ como una línea en un gráfico $xy$.

Las tareas de clasificación a menudo usan un modelo logístico fuertemente relacionado, que agrega una transformación adicional mapeando la salida de la función lineal al rango [0, 1], interpretado como “probabilidad de estar en la clase objetivo”. Los modelos lineales son rápidos de entrenar y generan una muy buena línea base contra la que comparar modelos más complejos. Los modelos más complejos pueden resultar atractivos, pero para la mayoría de problemas nuevos sería suficiente con considerar un modelo de regresión lineal simple.

Regresión lineal simple

Regresión lineal múltiple

Preguntas sobre el vídeo:

1. ¿Qué diferencia hay entre el modelo de regresión lineal simple y el modelo de regresión lineal múltiple?
2. ¿Por qué se usan matrices a la hora de programar modelos?
3. ¿Cómo podemos saber que una recta es mejor que otra en el modelo de regresión lineal?
4. ¿Por qué elevamos al cuadrado los errores en el modelo de regresión lineal?
5. ¿Por qué no se usa método de cuadrados ordinarios en inteligencia artificial?

¿Qué es regresión?

El análisis de regresión es la parte del aprendizaje supervisado que se ocupa de la predicción de valores numéricos continuos. En este caso, el objetivo del algoritmo es inferir¹ las relaciones entre las variables, que son previamente conocidas y que permiten ofrecer una predicción sobre la salida requerida. Para estos problemas, se utiliza un algoritmo de aprendizaje automático para construir un modelo que prediga un valor continuo. Es decir, dados los campos que definen una nueva instancia, el modelo predice un número real. Por ejemplo, el precio de una casa, el número de unidades vendidas de un producto, los ingresos potenciales de un posible cliente, el número de horas hasta el próximo fallo del sistema, etc.

La regresión es un problema matemático ampliamente conocido en el que se aplican técnicas que van desde las más simples (regresión lineal o polinómica) hasta las más complejas (Deep Learning, etc.) pero que se asemeja a un proceso de aproximación de funciones clásico en el que a partir de unas variables de entrada necesitamos encontrar aquella función que ofrezca la salida requerida. El proceso de validación de los modelos que resuelven problemas de regresión se basa en el uso de métricas de error, por ejemplo el error absoluto medio (MAE), el coeficiente de determinación (R^{2}), etc.

Información práctica

Preguntas sobre el vídeo:

1. ¿Qué simboliza el \(\epsilon\) en la fórumla \(Y = \beta_{0} + \beta_{1} X_{1} + \epsilon\)?
2. ¿Qué determina/simboliza el \(\beta_{1}\) en la fórumla \(Y = \beta_{0} + \beta_{1} X_{1} + \epsilon\)?
3. ¿A través de que método se obtienen los valores de \(\beta_{0}\) y \(\beta_{1}\)?

Regresión Logística

Regresión Logística

Regresión Logística por alvaro_opk

¿Se puede explicar cómo funciona y construye un modelo de machine learning a alguien totalmente ajeno al sector?

Vamos a hablar sobre un modelo cuyo objetivo es calcular la probabilidad de que ocurra un cierto evento.

Este tipo de problemas aparecen continuamente en la industría:

• 💸Probabilidad de impago
• 👱Probabilidad de que un cliente compre un producto

A modo de ejemplo imaginemos que buscamos un modelo que nos de la probabilidad de que una empresa suba en bolsa más de 5% este año.

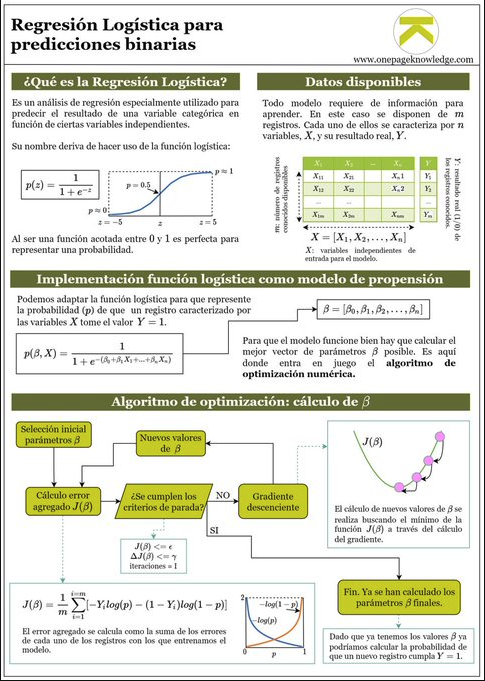
Uno de los modelos más sencillos y utilizados para resolver este tipo de problemas se llama ‘Regresión Logística’

¿De dónde viene ese nombre? Fácil. Porque se basa en la función logística.

Una de las propiedades de esta función es que está acotada entre 0 y 1 (ver imagen). Por tanto es muy apropiada para representar una probabilidad.

Veamos como esta función podría darnos la probabilidad de hacer un +5% que buscamos.

Función logística

Todo modelo de machine learning necesita datos de los que ‘aprender’ patrones.

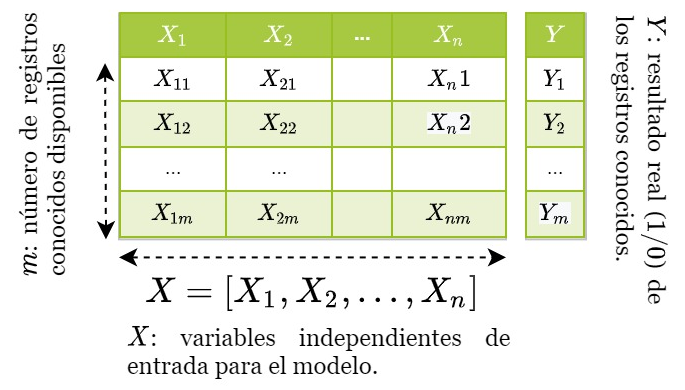
Imaginemos que tenemos la información de ‘m’ empresas y sabemos si subieron +5% en 2020 (Y=1) o no (Y=0).

También disponemos de características de las empresas (X)

Características de las empresas

• X1 podría ser la capitalización bursatil.
• X2 podría ser el número de empleados.
• X3 podría ser la variación del precio de la acción en 2019.

Y podríamos tener muchas más variables de este estilo. Cuando más relacionadas estén las variables con las futuras subidas en bolsa mejor.

Al final lo que estamos tratando de hacer es explicarle al modelo que pasó en el pasado con muchas empresas para que pueda buscar patrones y nos sirva para hacer inferencias de qué podría pasar en el futuro.

Bien. Ya tenemos datos y una función. Podemos combinar ambas cosas para crear una función logística.

La probabilidad ‘p’ depende de X (es decir, de los datos de la empresa en cuestión) y de unos parámetros BETA.

‘X’ los conocemos. Pero qué pasa con los valores BETA?

El kit de la cuestión es calcular los parámetros BETA que hagan que nuestra función para calcular ‘p’ funcione correctamente.

¿Cómo los calculamos? Aquí entra un algoritmo de optimización numérica.

Este proceso de cálculo lo podemos pintar de esta forma:

Lo vamos a ver paso a paso. Es más sencillo de lo que parece.

1.- Calcular BETA iniciales

Por simplificar imaginemos que nos los inventamos.

Al invertarnos los valores de los parámetros nuestra función no va a funcionar correctamente. Es decir, no va a calcular las probabilidades bien.

Pero ¿qué significa funcionar bien o mal?

2.- Cálculo del error J

J es una medida del error agregado que comete nuestra función logística.

La forma de calcular el error depende del algoritmo y modelo que estemos utilizando.

La cuestión es que de algún modo tenemos que cuantificar el error.

En el caso que estamos trabajando podríamos utilizar esta fórmula:

Fíjate que el error se cálcula como la suma de los errores cometidos en las ‘m’ empresas con las que estamos tratando de enseñar a nuestro modelo.

Por cierto, a la función J se le llama función de coste.

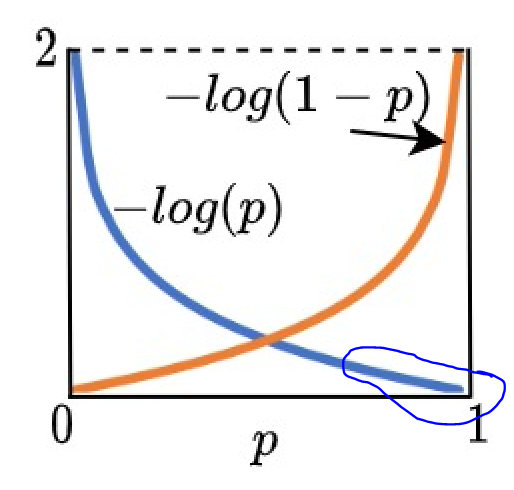
Imagina que uno de los ejemplos con los que estamos entrenando a nuestro modelo es una empresa que SI subió +5% en el 2020. Entonces Y=1.

Entonces el error asociado es -log(p) porque el término de la derecha desaparece.

¿Qué pasa entonces? Pues si nuestro modelo con parámetros inventados da una probabilidad cercana a 1 el error será bajo.

Si es cercana a 0 el error será grande.

Esto tiene sentido: sabemos que la empresa SI subió +5% por lo que nuestro modelo debería dar probabilidad alta.

3.- Criterios de parada

Esto son simplemente unas reglas para decidir si nuestro algoritmo de optimización debe terminar.

Por poner un ejemplo sencillo: podemos decidir que nuestro algoritmo pare cuando J sea menor que un valor umbral.

En la primera iteración nuestra función logística será muy mala y el valor de J será muy alto (es lo que tiene inventarse los parámetros…).

Por tanto tenemos que buscar unos parámetros mejores.

¿Cómo hacemos esto?

Vamos a uno de los puntos más importantes:

4.- Cálculo de nuevos parámetros beta

¿Te acuerdas cuando en el instituto tratabas de encontrar el mínimo de una función haciendo la derivada e igualándola a 0?

Pues es algo similar. En nuestro caso queremos minimizar el valor de J (el error agregado).

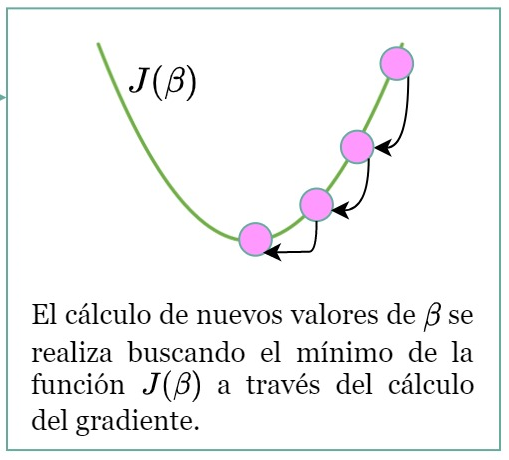
Ojo! Es similar pero no tan sencillo. Hay que calcular el gradiente (vector de derivadas parciales).

La cuestión es que gracias a las derivadas somos capaces de obtener unos nuevos parámetros BETA.

Estos nuevos parámetros serán mejores que los anteriores? En principio si.

Luego se repite el proceso:

• Con los nuevos parámetros volvemos a calcular el error J (que ahora será menor que antes)
• Vemos si cumplimos nuestros criterios de parada
• En caso negativo, volvemos a recurrir al gradiente para obtener nuevos Beta.

Y este proceso iterativo se repite hasta cumplir un criterio de parada.

Cuando esto ocurra tendremos unos parámetros BETA buenos para nuestra función logística.

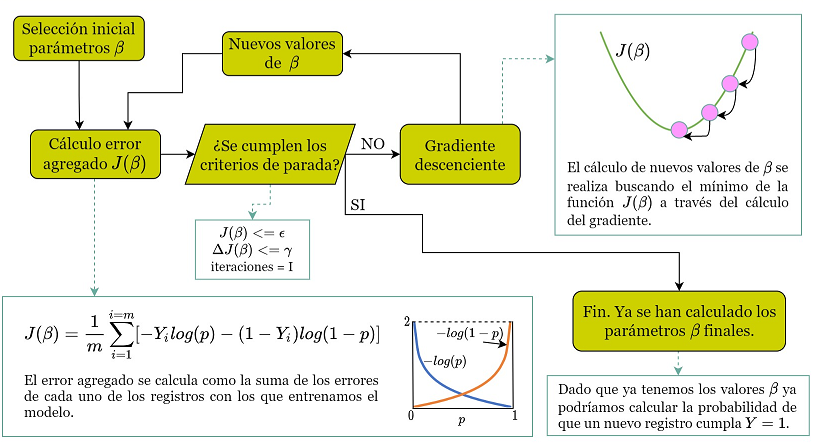
Y ya está. Ya tendríamos nuestra función para calcular p.

Para utilizarlo solo tendriamos que introducir los valores de X de la empresa que queramos y obtener la probabilidad de que suba +5% este año.

Al final todo es cuestión de construir una función matemática más o menos compleja que depende de ciertos parámetros (ojo, pueden ser millones de parámetros)

Cuando se habla de ‘entrenar un modelo’ se hace referencia al cálculo de esos parámetros desconocidos de nuestra función.

Si has llegado hasta aquí enhorabuena y muchas gracias.

Espero que te haya servido para hacerte una idea clara de que implica construir un modelo de este estilo.

A veces cuando se habla de esta materia parece magia negra. Todo es matemáticas y cálculo computacional.

Preguntas sobre el vídeo:

1. ¿En qué se diferencia la regresión lineal de la regresión logística?
2. ¿Qué es el BMI?
3. ¿Cuál es la función logística?
4. ¿Qué otro nombre tiene la función logística?
5. ¿Con que algoritmo se optimiza el error en la regresión logística?

Árboles de Decisión

Los modelos basados en árboles son probablemente el segundo tipo de modelo más común por detrás de la regresión lineal y el más importante modelo de clasificación. Aprenden a categorizar o retroceder construyendo una estructura extremadamente grande de bloques if/else anidados, dividiendo el conjunto de datos en diferentes regiones en cada bloque if/else. El entrenamiento determina exactamente dónde ocurren estas divisiones y qué valor se asigna en cada región hoja. Por ejemplo, si intentamos determinar si un sensor de luz está al sol o a la sombra, podríamos entrenar un árbol de profundidad 1 con la configuración final aprendida:

si (valor_sensor> 0,698), entonces devuelve 1; de lo contrario, devuelve 0 ;

El modelo XGBoost basado en árboles de decisión se usa comúnmente como una implementación sencilla. Inicialmente es mejor probar modelos simples para posteriormente migrar a modelos más complejos.

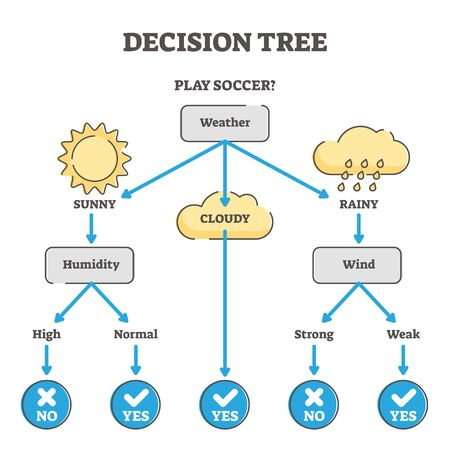Árbol de decisión para jugar a futbol

Árboles de Decisión

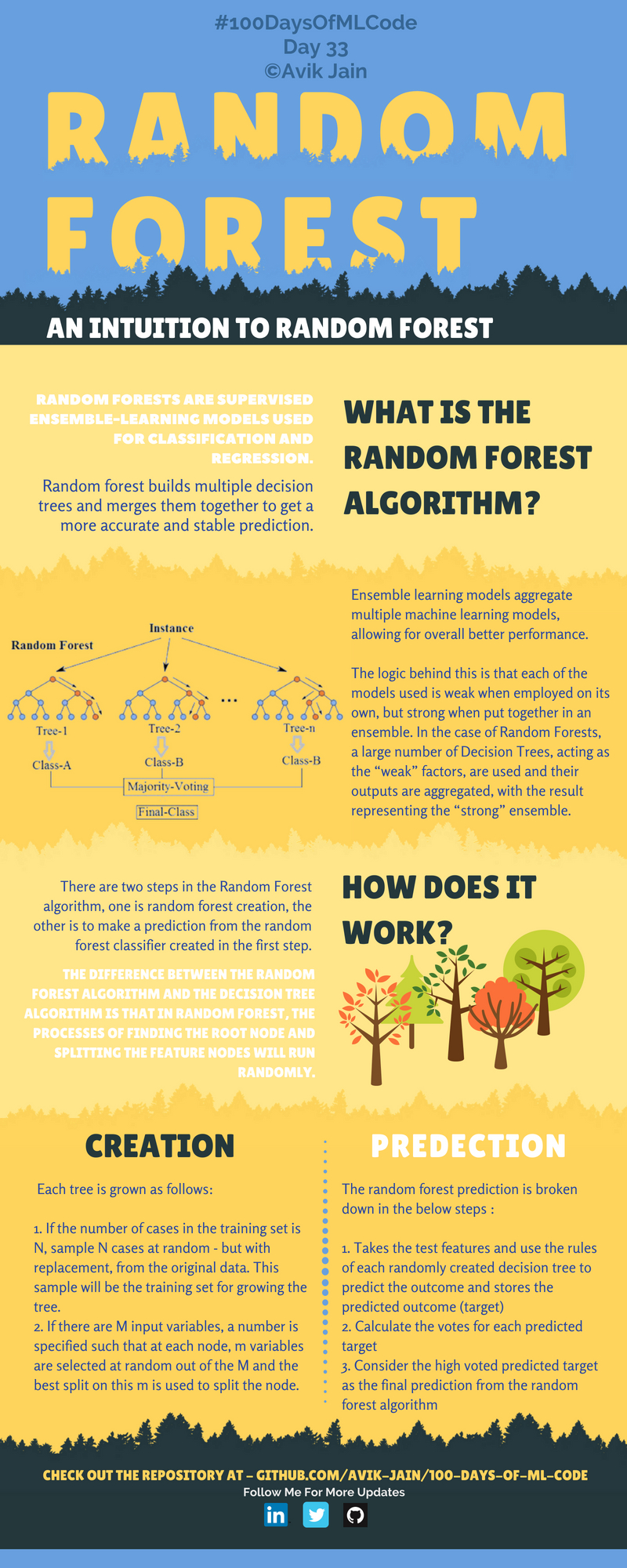Random forest

Preguntas sobre el vídeo:

1. ¿Por qué decide el árbol de decisión que la mejor variable a usar es el salario de los clientes?
2. ¿Qué es el OverallQual?
3. ¿Cuales son los pros de los árboles de decisión?
4. ¿Cuáles son los contras de los árboles de decisión?

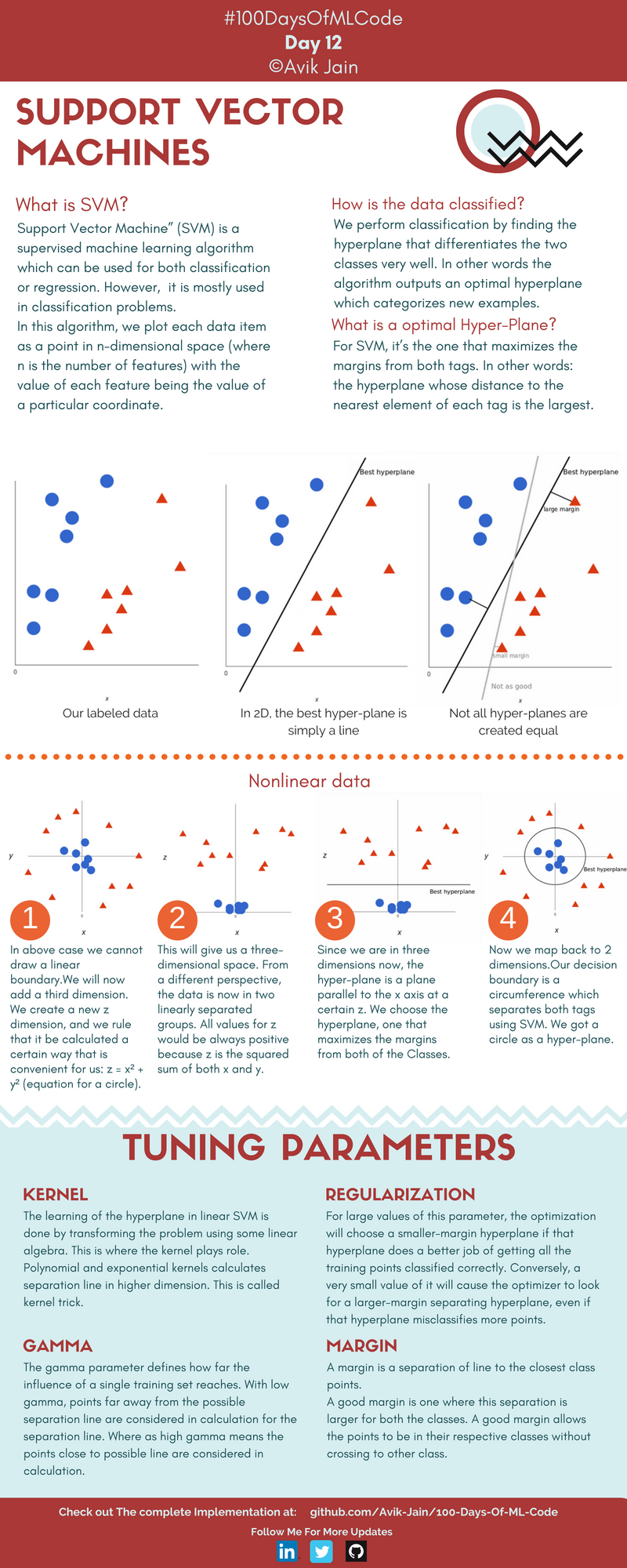
Máquinas de Vector Soporte (SVM)

Regresión Logística

Preguntas sobre el vídeo:

1. ¿Qué significan las siglas en inglés SVM?
2. ¿Es SVM aprendizaje supervisado o no supervisado? ¿Por qué?
3. ¿Cómo explica que se obtiene la recta que separa los dos grupos?
4. ¿Por qué llama hiperplano a la recta?

Bibliografía

• https://twitter.com/alvaro_opk/status/1358376337979944960
• https://github.com/cristinagom/machinelearning/

1. Extraer un juicio o conclusión a partir de hechos, proposiciones o principios, sean generales o particulares. ↩